Administrivia

Administrivia Setup

Lectures

1. Game Engines Overview

Overview Module Overview Game Engine Links

2. Rendering Engine

Rendering Overview Graphics Libraries 2D Rendering 3D Rendering Techniques

3. Scene Graph

Introduction SG Contents SG Traversal SG APIs SG Benefits

4. Collision Detection

Introduction After or Before A Posteriori A Priori

5. Physics

Introduction Collision Response Soft-body Dynamics Other Components

6. Networking

Network Overview

7. Which Engine?

Which Engine?

Assessment

Assessment

Mid-Module Evaluation

A Priori

There are a couple of basic techniques we can use to try to avoid tunnelling. We can make the speed of objects low enough that they can never tunnel through another object and we can make sure every object is too big to tunnel through. This is hardly a satisfying approach, the last thing we want to do in a game is limit movement speed and clutter the screen with huge objects just so the objects don’t tunnel through each other.

Instead we use a more complex approach known as continious collision detection.

Continuous Collision Detection

(swiped from https://www.toptal.com/game/video-game-physics-part-ii-collision-detection-for-solid-objects)

Continuous collision detection techniques attempt to find when two bodies collided between the previous and the current step of the simulation. They compute the time of impact, so we can then go back in time and process the collision at that point.

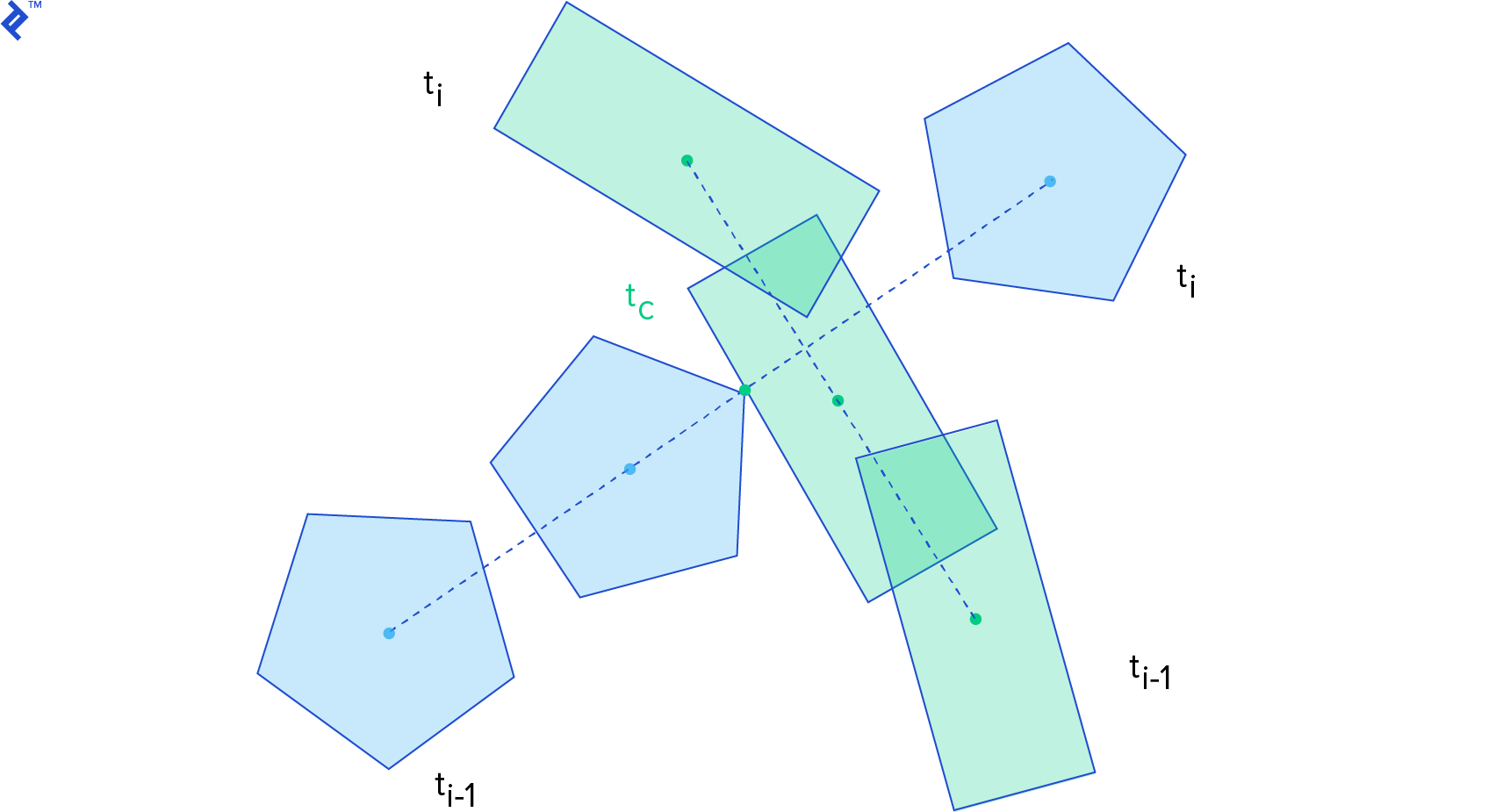
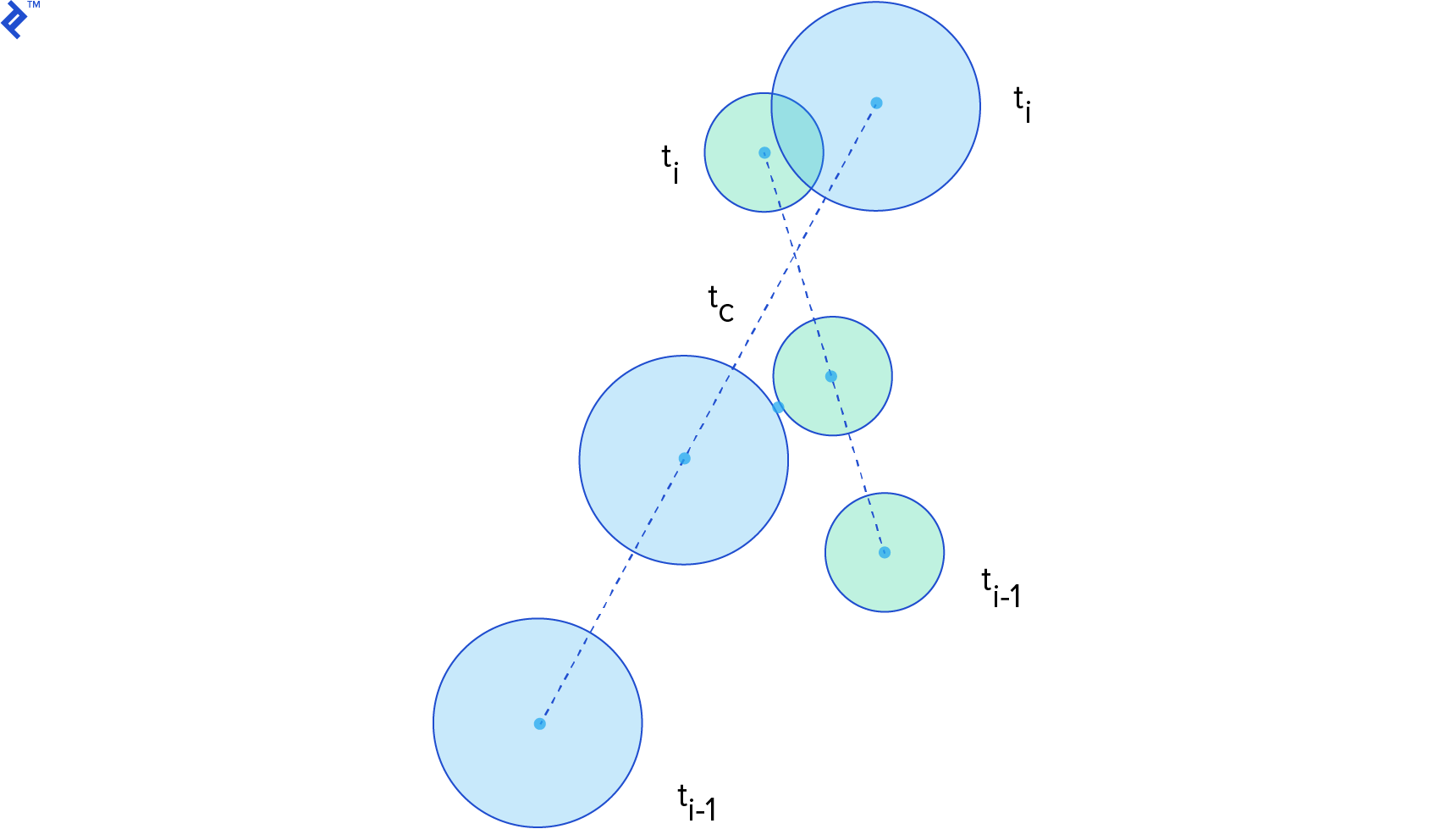
The time of impact (or time of contact) t_c is the instant of time when the distance between two bodies is zero. If we can write a function for the distance between two bodies along time, what we want to find is the smallest root of this function. Thus, the time of impact computation is a root-finding problem.

For the time of impact computation, we consider the state (position and orientation) of the body in the previous step at time t_i-1, and in the current step at time t_i. To make things simpler, we assume linear motion between the steps.

continuous collision detection

Let’s simplify the problem by assuming the shapes are circles. For two circles C₁ and C₂, with radius r₁ and r₂, where their center of mass x₁ and x₂ coincide with their centroid (i.e., they naturally rotate about their center of mass), we can write the distance function as:

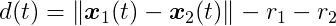
continuous collision detection

Considering linear motion between steps, we can write the following function for the position of C₁ from t_i-1 to t_i

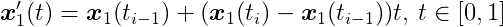
continuous collision detection

It is a linear interpolation from x_1(ti-1) to x_1(ti). The same can be done for x₂. For this interval we can write another distance function:

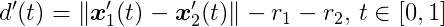
continuous collision detection

Set this expression equal to zero and you get a quadratic equation on t. The roots can be found directly using the quadratic formula. If the circles don’t intersect, the quadratic formula will not have a solution. If they do, it might result in one or two roots. If it has only one root, that value is the time of impact. If it has two roots, the smallest one is the time of impact and the other is the time when the circles separate. Note that the time of impact here is a number from 0 to 1. It is not a time in seconds; it is just a number we can use to interpolate the state of the bodies to the precise location where the collision happened.

continuous collision detection

Continuous Collision Detection for Non-Circles

Writing a distance function for other kinds of shapes is difficult, primarily because their distance depends on their orientations. For this reason, we generally use iterative algorithms that move the objects closer and closer on each iteration until they are close enough to be considered colliding.

The conservative advancement algorithm moves the bodies forward (and rotates them) iteratively. In each iteration it computes an upper bound for displacement. The original algorithm is presented in Brian Mirtich’s PhD Thesis (section 2.3.2), which considers the ballistic motion of bodies. This paper by Erwin Coumans (the author of the Bullet Physics Engine) presents a simpler version that uses constant linear and angular velocities.

The algorithm computes the closest points between shapes A and B, draws a vector from one point to the other, and projects the velocity on this vector to compute an upper bound for motion. It guarantees that no points on the body will move beyond this projection. Then it advances the bodies forward by this amount and repeats until the distance falls under a small tolerance value.

It may take too many iterations to converge in some cases, for example, when the angular velocity of one of the bodies is too high.

Links

Improve this page