A Posteriori
Detecting Collisions After The Fact
A Posteriori collision detection, in its simplest form, updates the positions of objects within the scene and then checks for collisions.
End Location Comparisons
There are a number of methods for doing this, the simplest is a comparison of the final locations of each object looking for overlaps. There are a number of techniques for doing this.
2D
Tiles
Where object within a game are located within tiles on a board (i.e. chess) It is a simple case to detect if the objects have the same location (i.e. square A5).
Bounding Circles
We can bound our sprites with circles.

We can detect if two circles are overlapping if the distance between the centres of the circles is less than the sum of the radii of those circles.
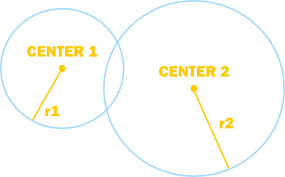
This is easy to calculate if ((r1+r2)<sqrt((x1-x2)^2+(y1-y2)^2)) then collision = true.
In practice we usually square each side to avoid the computationally expensive sqrt().
if (r1+r2)^2 < ((x1-x2)^2 + (y1-y2)^2)
This makes the calculation much faster.
Bounding Squares
An alternative to bounding circles is bounding rectangles. This is slightly slower to calculate but may give more accurate results as sprites tend to be more rectangular than circular.

Origin at top left, x increasing to the right, y increasing downwards.
Assume two rectangles A & B, located at A.x, A.y, B.x, B.y which equates to the top left corner of the respective squares. Each square has a width and a height.
Here we can detect a collision between two rectangles if all the following conditions are true.
- A.x + A.width > B.x
- A.x < B.x + B.width
- A.y + A.height > B.y
- A.y < B.y + B.height
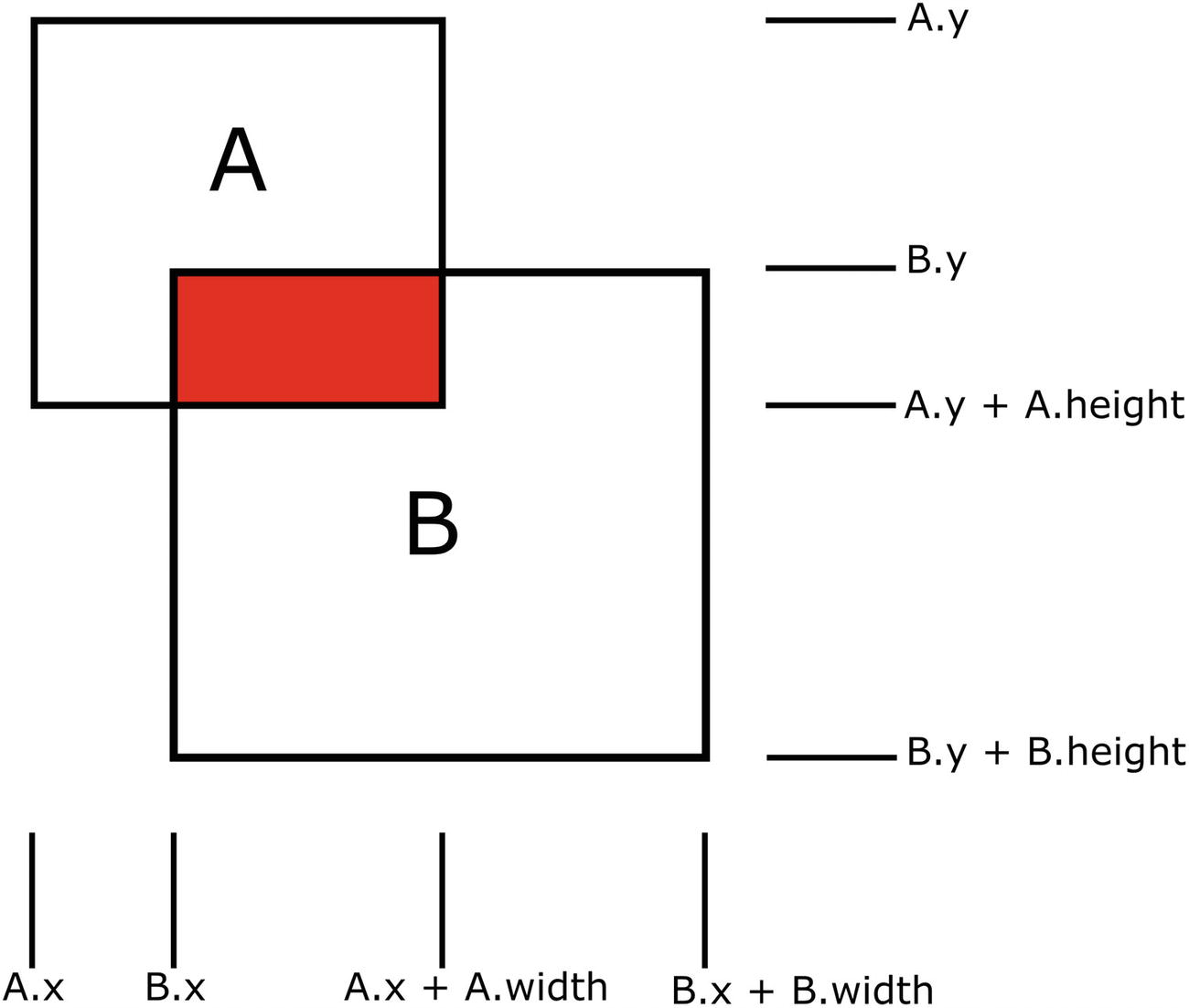
Alternatively we can say that if any of those four are not true there is no collision, which is a faster calculation since it stops as soon as it fails.
This process only works with boxes aligned to the axis, if either rectangle is rotated the calculations become more complex and computationally expensive.
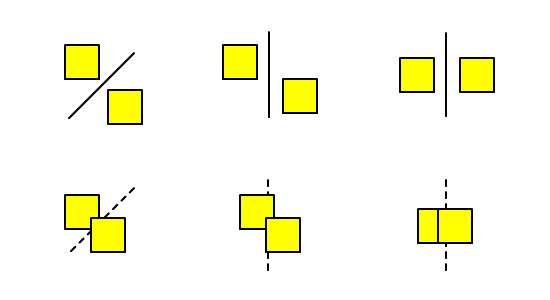
Separating Axis Theorem
The Separating Axis Theorem (SAT for short) essentially states if you are able to draw a line to separate two polygons, then they do not collide. It’s that simple.
3D
3D collision detection uses the same techniques but they are more computationally intensive due to the extra dimension.
Tunnelling Problem
There is a big problem with A Posteriori collision detection. It is possible for one object to pass through another if its movement takes it completely past the object in a single update.
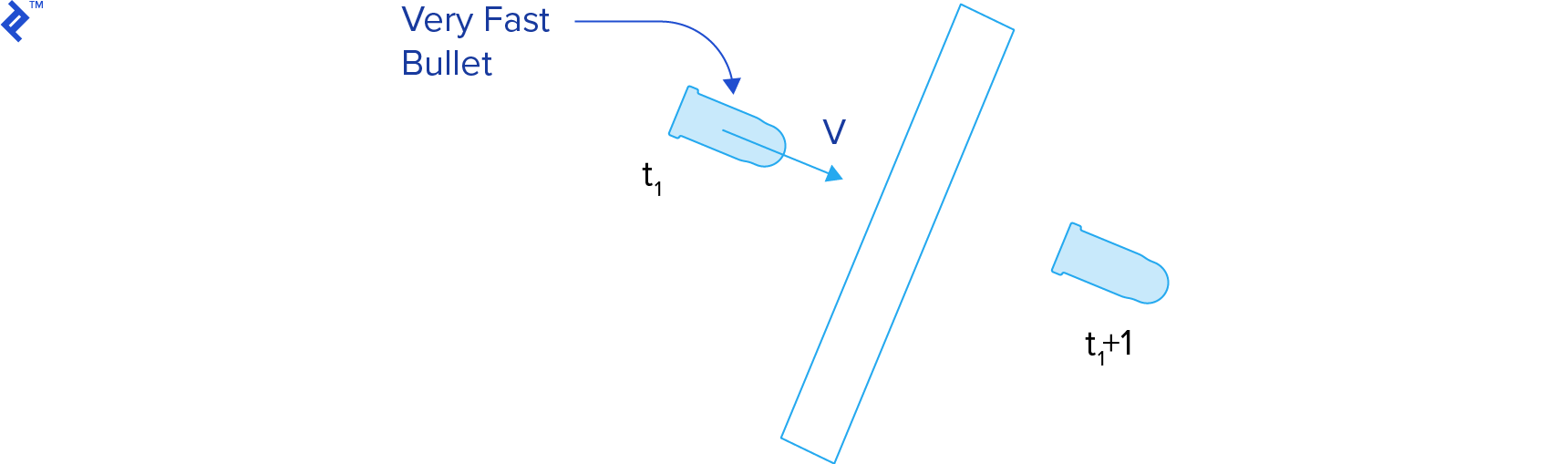
In the example above in the first update the bullet is one side of the wall and moving at a high velocity. After the next update the velocity has taken the bullet to the other side of the wall. No collision is detected in either update. This is known as tunnelling.

To avoid tunnelling we need to use continuous collision detect, a priori detection.
Collision Performance
We can speed up collision detection by separating it in to two phases. I the first phase, the broad phase, a simple rough test is performed to eliminate cases where collisions do not occur, leaving fewer cases that need detailed evaluation in a second narrow phrase.
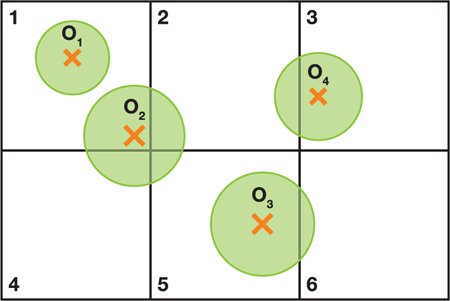
With the diagram above we can easily identify that two circles which do not share a common region cannot be colliding with each other. Circle 1 is entirely within area 1, it cannot collide with any circle which is not at least partly in area 1. So the only circle it might be colliding with O2. We only need to carry out the calculation O1 and O2. We then move on to which circles (other than O1) share an area with O2 and so on.